Brachistochrone curve
A Brachistochrone curve (Gr. βράχιστος, brachistos - the shortest, χρόνος, chronos - time), or curve of fastest descent, is the curve between two points that is covered in the least time by a point-like body that starts at the first point with zero speed and is constrained to move along the curve to the second point, under the action of constant gravity and assuming no friction.
Contents |
The brachistochrone is the cycloid
Given two points A and B, with A not lower than B, there is just one upside down cycloid that passes through A with infinite slope, passes also through B and does not have maximum points between A and B. This particular inverted cycloid is a brachistochrone curve. The curve does not depend on the body's mass or on the strength of the gravitational constant.
The problem can be solved with the tools from the calculus of variations.
If the body is given an initial velocity at A, or if friction is taken into account, the curve that minimizes time will differ from the one described above.
Johann Bernoulli's solution
According to Fermat’s principle: The actual path between two points taken by a beam of light is the one which is traversed in the least time. Johann Bernoulli used this principle to derive the brachistochrone curve by considering the trajectory of a beam of light in a medium where the speed of light increases following a constant vertical acceleration (that of gravity g).[1]
The conservation law can be used to express the speed of a body in a constant gravitational field as:
 ,
,
where y represents the vertical distance the body has fallen. By conservation of energy the speed of motion of the body along an arbitrary curve does not depend on the horizontal displacement.
Johann Bernoulli noted that the law of refraction gives a constant of the motion for a beam of light in a medium of variable density:
 ,
,
where vm is the constant and  represents the angle of the trajectory with respect to the vertical.
represents the angle of the trajectory with respect to the vertical.
The equations above allow us to draw two conclusions:
- At the onset, when the particle speed is nil, the angle must be nil. Hence, the brachistochrone curve is tangent to the vertical at the origin.
- The speed reaches a maximum value when the trajectory becomes horizontal and the angle θ = 90°.
To keep things simple we can assume that the particle (or the beam) with coordinates (x,y) departs from the point (0,0) and reaches maximum speed after a falling a vertical distance D. So,
 .
.
Rearranging terms in the law of refraction and squaring gives:
which can be solved for dx in terms of dy:
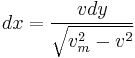 .
.
Substituting from the expressions for v and vm above gives:
which is the differential equation of an inverted cycloid generated by a circle of diameter D.
Johann's brother Jakob showed how 2nd differentials can be used to obtain the condition for least time. A modernized version of the proof is as follows. If we make a negligible deviation from the path of least time then, for the differential triangle formed by the displacement along the path and the horizontal and vertical displacements,
 .
.
On differentiation with dy fixed we get,
 .
.
And finally rearranging terms gives,
where the last part is just the change in distance for given change in time for 2nd differentials. Now consider the changes along the two neighboring paths in the figure below for which the horizontal separation between paths along the central line is d2x (the same for both the upper and lower differential triangles). Along the old and new paths, the parts that differ are,
For the path of least times these times are equal so for their difference we get,
And the condition for least time is,
History
Johann Bernoulli posed the problem of the brachistochrone to the readers of Acta Eruditorum in June, 1696. He published his solution in the journal in May of the following year, and noted that the solution is the same curve as Huygens's tautochrone curve. After deriving the differential equation for the curve by the method given above, he went on to show that it does yield a cycloid.[2][3] But his proof is marred by the fact that he uses a single constant instead of the three constants, vm, 2g and D, above. Five mathematicians responded with solutions: Isaac Newton, Jakob Bernoulli (Johann's brother), Gottfried Leibniz, Ehrenfried Walther von Tschirnhaus and Guillaume de l'Hôpital. Four of the solutions (excluding l'Hôpital's) were published in the same edition of the journal as Johann Bernoulli's. In his paper Jakob Bernoulli gave a proof of the condition for least time similar to that above before showing that its solution is a cycloid.[2]
In an attempt to outdo his brother, Jakob Bernoulli created a harder version of the brachistochrone problem. In solving it, he developed new methods that were refined by Leonhard Euler into what the latter called (in 1766) the calculus of variations. Joseph-Louis de Lagrange did further work that resulted in modern infinitesimal calculus.
Galileo tried to solve a similar problem for the path of the fastest descent from a point to a wall in his Two New Sciences in 1638. He draws the conclusion (Third Day, Theorem 22, Prop. 36) that the arc of a circle is faster than any number of its chords,[4]
- "From the preceding it is possible to infer that the quickest path of all [lationem omnium velocissimam], from one point to another, is not the shortest path, namely, a straight line, but the arc of a circle.
- ...
- Consequently the nearer the inscribed polygon approaches a circle the shorter is the time required for descent from A to C. What has been proven for the quadrant holds true also for smaller arcs; the reasoning is the same."
We are warned earlier in the Discourses (just after Theorem 6) of possible fallacies and the need for a "higher science." In this dialogue Galileo reviews his own work. The actual solution to Galileo's problem is half a cycloid. Galileo studied the cycloid and gave it its name, but the connection between it and his problem had to wait for advances in mathematics.
See also
- Calculus of variations
- Beltrami identity
- Cycloid
- Tautochrone curve
- Catenary
- uniformly accelerated motion
References
- ^ Babb, Jeff; Currie, James (July 2008), "The Brachistochrone Problem: Mathematics for a Broad Audience via a Large Context Problem", TMME 5 (2&3): 169–184, http://www.math.umt.edu/tmme/vol5no2and3/TMME_vol5nos2and3_a1_pp.169_184.pdf
- ^ a b Struik, J. D. (1969), A Source Book in Mathematics, 1200-1800, Harvard University Press, ISBN 0691023972
- ^ Herman Erlichson (1999), "Johann Bernoulli's brachistochrone solution using Fermat's principle of least time", Eur. J. Phys. 20: 299–304, doi:10.1088/0143-0807/20/5/301, http://www.iop.org/EJ/abstract/0143-0807/20/5/301
- ^ Galileo Galilei (1638), Discourses regarding two new sciences, p. 239, http://galileoandeinstein.physics.virginia.edu/tns_draft/tns_160to243.html
External links
- Weisstein, Eric W., "Brachistochrone Problem" from MathWorld.
- Courbe Brachistrocrone (in French with excellent animated examples)
- The Brachistochrone, Whistler Alley Mathematics.
- Table IV from Bernoulli's article in Acta Eruditorum 1697
- Brachistochrones by Michael Trott and Brachistochrone Problem by Okay Arik, Wolfram Demonstrations Project.
- The Brachistochrone problem at MacTutor






